Viral Respiratory Epidemic Modeling of Societal Segregation Based on Vaccination Status

December 31 | Posted by mrossol | Math/Statistics, Science, Vaccine

Source: Cureus | Viral Respiratory Epidemic Modeling of Societal Segregation Based on Vaccination Status | Article

Published: December 14, 2023

DOI: 10.7759/cureus.50520

Peer-Reviewed

Cite this article as: Hickey J, Rancourt D G (December 14, 2023) Viral Respiratory Epidemic Modeling of Societal Segregation Based on Vaccination Status. Cureus 15(12): e50520. doi:10.7759/cureus.50520

Abstract

Background: Societal segregation of unvaccinated people from public spaces has been a novel and controversial coronavirus disease 2019 (COVID-19)-era public health practice in many countries. Models exploring potential consequences of vaccination-status-based segregation have not considered how segregation influences the contact frequencies in the segregated groups. We systematically investigate implementing effects of segregation on population-specific contact frequencies and show this critically determines the predicted epidemiological outcomes, focusing on the attack rates in the vaccinated and unvaccinated populations and the share of infections among vaccinated people that were due to contacts with infectious unvaccinated people.

Methods: We describe a susceptible-infectious-recovered (SIR) two-population model for vaccinated and unvaccinated groups of individuals that transmit an infectious disease by person-to-person contact. The degree of segregation of the two groups, ranging from zero to complete segregation, is implemented using the like-to-like mixing approach developed for sexually transmitted diseases, adapted for presumed severe acute respiratory syndrome coronavirus 2 (SARS‑CoV‑2) transmission. We allow the contact frequencies for individuals in the two groups to be different and depend, with variable strength, on the degree of segregation.

Results: Segregation can either increase or decrease the attack rate among the vaccinated, depending on the type of segregation (isolating or compounding), and the contagiousness of the disease. For diseases with low contagiousness, segregation can cause an attack rate in the vaccinated, which does not occur without segregation.

Interpretation: There is no predicted blanket epidemiological advantage to segregation, either for the vaccinated or the unvaccinated. Negative epidemiological consequences can occur for both groups.

Introduction

Models can be used to investigate infectious disease dynamics under different hypotheses about the characteristics of a disease and the effects of health policy. In this endeavour, there are advantages to working with the simplest possible but sufficiently realistic models [1,2], where one should exclude simple models that are not sufficiently realistic for the intended application, either because of their structure or because of incorrect assumptions about the underlying mechanisms. Following this approach, researchers have extended the foundational simple susceptible-infectious-recovered (SIR)-type model to explore diseases with birth and death dynamics, maternal- or vaccine-derived immunity, latency of infection, patterns of contact mixing between different societal groups, and so on [3-7], and to study the effect of isolating vulnerable individuals from the general population during a pandemic, in the absence of vaccination [8].

Recently, SIR models of epidemic dynamics have been implemented with two interacting societal groups (vaccinated and unvaccinated) to examine epidemic outcomes for variable degrees of interaction between the two groups, including whether the unvaccinated put the vaccinated unduly or disproportionately at risk, using epidemiological parameters intended to be representative of severe acute respiratory syndrome coronavirus 2 (SARS‑CoV‑2) [9-12]. These prior implementations regarding groups differentiated by vaccination status take the contact frequencies of the majority and socially excluded groups to be equal and held constant, irrespective of the degree of segregation (or exclusion or “like-to-like mixing”), which is not realistic.

Here, we implement population-specific contact frequencies that can be different for the two groups and can either increase or decrease with increasing segregation. This is necessary because, for example, in many actual regulatory policies, the excluded unvaccinated group is barred from public venues or services where people gather and from public transport where people are in close proximity for various durations. In general, the contact frequency of the excluded group decreases with increasing segregation if isolation is in effect, and increases with increasing segregation if the excluded individuals are crowded together. Implementing this essential model feature gives rise to the more complex behaviour of the attack rates in the vaccinated and unvaccinated populations (A_v and A_u, respectively), which can increase or decrease, or rise to a maximum before decreasing, as the two groups are increasingly segregated. This is also true for the share (B_v) of infections among vaccinated people that are due to contact with infectious unvaccinated people.

This article was previously posted to the medRxiv preprint server on August 23, 2022, and revised versions were posted to medRxiv on November 28, 2022, July 6, 2023, July 19, 2023, and October 31, 2023.

Materials & Methods

Model design

We adopt the standard SIR framework in a structure with two sub-populations. If a susceptible person (S) comes into contact with an infectious person (I), the susceptible person can become infectious, and infectious people eventually recover (R) and become permanently immune.

We divide the population into two groups: vaccinated and unvaccinated. Vaccination is “all or nothing”, such that a proportion, VE, of the vaccinated population is immune (is in the R state from the outset of the simulation), where the parameter VE represents vaccine efficacy. The model also includes a natural immunity parameter, NI, equal to the proportion of unvaccinated that are immune from the outset due to previous infection [9].

The model consists of the following six differential equations:

d S u d t = - c u β u S u [f u v I v N v + f u u I u N u]

d I u d t = c u β u S u [f u v I v N v + f u u I u N u] - γ u I u

d R u d t = γ u I u

d S v d t = - c v β v S v [f v u I u N u + f v v I v N v]

d I v d t = c v β v S v [f v u I u N u + f v v I v N v] - γ v I v

d R v d t = γ v I v

S_u, I_u, and R_u represent the number of susceptible, infectious, and recovered unvaccinated people, at time t. N_u represents the total number of unvaccinated people. c_u represents the population-specific contact frequency (number of contacts per unit time) of unvaccinated people. β_u is the probability that a susceptible unvaccinated person becomes infected upon contact with an infectious person (regardless of whether the infectious person is vaccinated or unvaccinated). γ_u is the rate at which infected unvaccinated people recover from infection. The quantities S_v, I_v, R_v, N_v, c_v, β_v, and γ_v are defined equivalently, for vaccinated people.

f_ij is the probability that a person of type i (either u or v) has contact with a person of type j (either u or v) and is modulated by a parameter, η, which controls the degree of segregation between vaccinated and unvaccinated people (see Appendix 1 for technical details). When η = 0, there is no segregation, and the two groups mix randomly. When η = 1, there is complete segregation, such that the vaccinated only come into contact with other vaccinated, and the unvaccinated only come into contact with other unvaccinated.

The parameter η follows from Garnett and Anderson [1], who modelled sexually transmitted disease spread in a population divided into groups with different frequencies of sexual contact. They take the contact frequency to be a constant characteristic of the individuals within a group. However, contact frequency is not generally and solely an intrinsic individual characteristic [13].

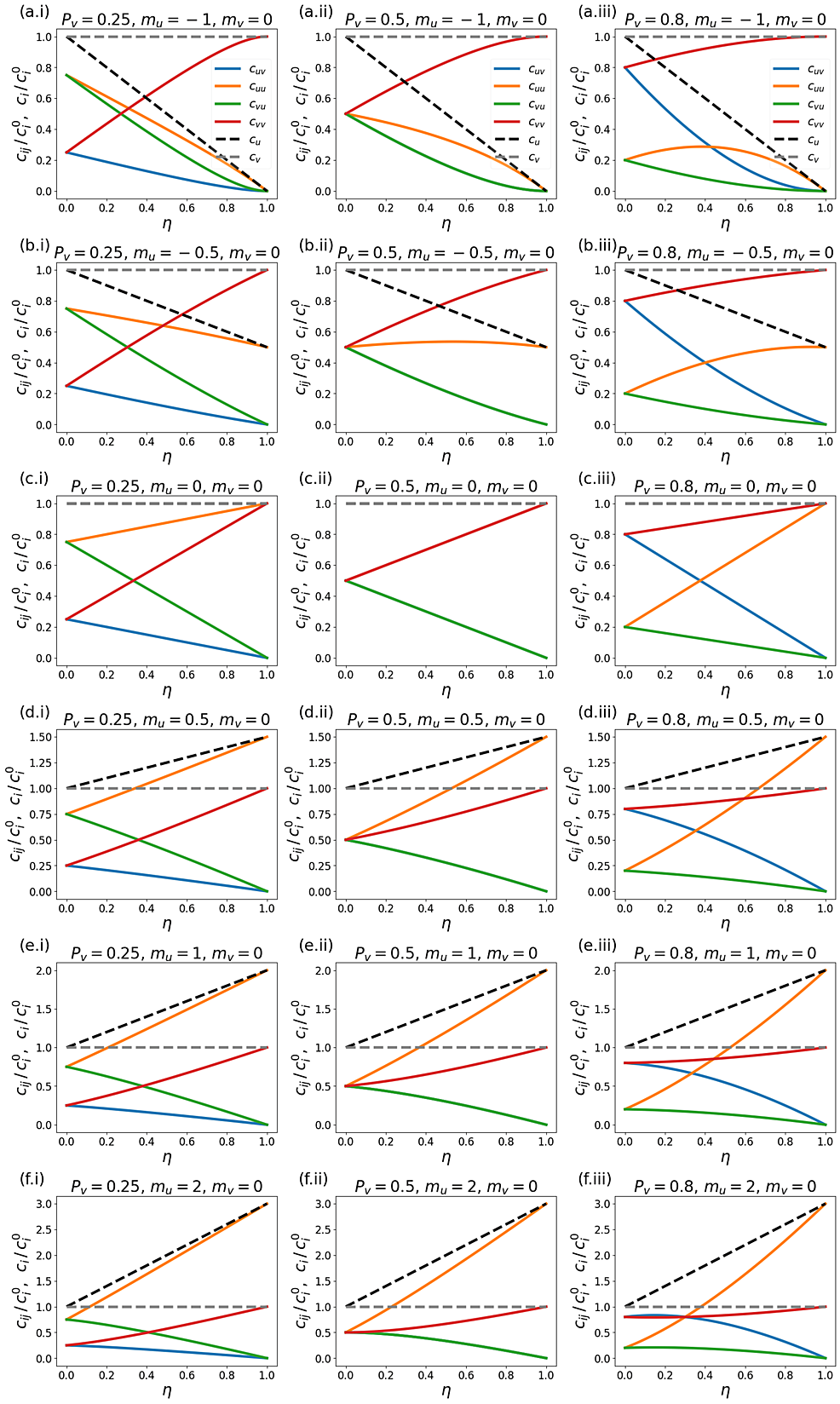
In our model, the population-specific contact frequencies of the vaccinated and unvaccinated individuals (c_v and c_u, respectively) can increase, decrease, or remain constant as the two groups are segregated. We implement a new approach to achieve this: we keep the first two terms in Taylor expansions of c_vand c_u versus η (c_v = (1 + m_vη) and c_u = (1 + m_uη); see Equations A3 in Appendix 1). Thus, m_v and m_u determine the degree of increase or decrease of the contact frequency in either group, as η is increased.

For example, when m_u < 0, as segregation is increased, the contact frequency of unvaccinated people decreases. This corresponds to a segregation policy that excludes unvaccinated people from public spaces such as restaurants, cinemas, workplaces, airplanes, trains, etc. [14-17]. Conversely, m_u > 0 corresponds to a segregation policy that increases contact between unvaccinated people; for example, by requiring returning unvaccinated travelers to stay in designated facilities [18-20].

In principle, the vaccinated and unvaccinated contact frequencies may be different even when the two groups are completely unsegregated. The unsegregated (η = 0) contact frequencies are set by the parameters $c_{v}^{0}$ and $c_{u}^{0}$ .

As can be seen from the six differential equations defining our model, there are two “β parameters”, two “c parameters” and two “γ parameters” in our model. Since each β parameter always occurs as part of a product with its respective cparameter, the β parameters can freely be set equal to 1. We set β_v = β_u = 1 in this paper, without any loss of generality. This implies that, by definition (since β = 1), the contact frequencies “c” in our model are conceptually for contacts that are of sufficiently close proximity and long duration that an infection is guaranteed to occur when a susceptible and an infectious person meet [7,8]. For a more contagious virus, more of an individual’s contacts are long and close enough that transmission would be guaranteed, corresponding to higher $c_{v}^{0}$ and $c_{u}^{0}$ . In other words, setting β_v = β_u = 1 is equivalent to redefining “c” as the product “βc”, thus eliminating a redundant parameter, without any loss of generality.

The model of Fisman et al. [9] is the special case of our model with m_u = m_v = 0, $c_{v}^{0} β_{v} = c_{u}^{0} β_{u}$ and γ_v = γ_u in which case the equal contact frequencies of both vaccinated and unvaccinated remain constant regardless of the level of segregation. Such an implementation does not represent how segregation has been applied during the coronavirus disease 2019 (COVID-19) era in Canada and many countries [14-17,21], since unvaccinated people were excluded from public spaces while vaccinated people were allowed access, thus changing venues and opportunities for contact as segregation is imposed.

Throughout this paper, “contact frequency” refers to the frequency of infectious contacts, since the probability of infection per infectious-susceptible contact is set equal to 1 without loss of generality (see Appendix 1).

Model parameterization

The parameters of our model are listed in Table 1 and calculated quantities are given in Table 2. Technical details of the model are in Appendix 1.

Parameter description	Symbol	Typical value	Bound
Degree of segregation of vaccinated and unvaccinated groups	η	(varied)	0 to 1
Contact frequency of vaccinated people when η = 0	$c_{v}^{0}$	300 contacts/yr	≥ 0
Contact frequency of unvaccinated people when η = 0	$c_{u}^{0}$	300 contacts/yr	≥ 0
Probability of transmission per contact between a susceptible vaccinated person and an infected person	β_v	1	0 to 1
Probability of transmission per contact between a susceptible unvaccinated person and an infected person	β_u	1	0 to 1
Degree of increase ( $m_{v} > 0$ ) or decrease ( $m_{v} < 0$ ) of vaccinated contact frequency as a function of η	$m_{v}$	0	≥ -1
Degree of increase ( $m_{u} > 0$ ) or decrease ( $m_{u} < 0$ ) of unvaccinated contact frequency as a function of η	$m_{u}$	varied	≥ -1
Rate of recovery from infection of a vaccinated person (per year)	γ_v	73 yr^-1	≥ 0
Rate of recovery from infection of an unvaccinated person (per year)	γ_u	73 yr^-1	≥ 0
Population fraction of vaccinated people	P_v	0.8	0 to 1
Vaccine efficacy	VE	0.8	0 to 1
Proportion of unvaccinated population with natural immunity	NI	0.2	0 to 1
Population of entire society	N	10⁷	> 0

Table 1: Model parameters

Name	Symbol
Attack rate in the vaccinated population	A_v
Attack rate in the unvaccinated population	A_u
Attack rate in the overall population (vaccinated and unvaccinated)	A_t
Share of infections among vaccinated people that were due to contacts with infectious unvaccinated people	B_v

Table 2: Quantities calculated from model results

Mathematical definitions of the quantities in Table 2 can be found in Appendix 1, Section A1.3.

Analysis

The attack rate among the vaccinated population is defined as the proportion of initially susceptible vaccinated people who become infected during the epidemic:

$A_{v} = \frac{S_{v} (t_{0}) - S_{v} (t_{f})}{S_{v} (t_{0})}$

where S_v(t0) is the number of susceptible vaccinated people at the beginning of the epidemic and S_v(t_f) is the number of susceptible vaccinated people remaining once there are no longer any infectious people in the entire (vaccinated and unvaccinated) population. A_u is defined equivalently, for the unvaccinated, replacing the v subscripts with u in the equation A_v above.

The overall attack rate for the full (vaccinated plus unvaccinated population) is:

$A_{t} = \frac{(S_{v} (t_{0}) + S_{u} (t_{0})) - (S_{v} (t_{f}) + S_{u} (t_{f}))}{S_{v} (t_{0}) + S_{u} (t_{0})}$

We also define B_v as the share of infections among vaccinated people that were due to contact with infectious unvaccinated people (see Equation A6 of Appendix 1).

We focus on segregation types that are targeted at the unvaccinated group. We assume, for simplicity, that segregation has no impact on the contact frequency of vaccinated people (m_v = 0). We also assume that the contact frequencies in both groups are the same when there is no segregation ( $c_{v}^{0} = c_{u}^{0}$ ). We use the same values as used by Fisman et al. [9] for the remaining parameters: P_v = 0.8, VE = 0.8, NI = 0.2, γ_v = γ_u = 73 yr^-1, and N = 10⁷. These values were intended to be representative of COVID-19 and vaccination; in particular, the recovery rate of 73 yr^-1 is equivalent to a recovery time of five days [22,23] and is assumed to be the same for vaccinated and unvaccinated people.

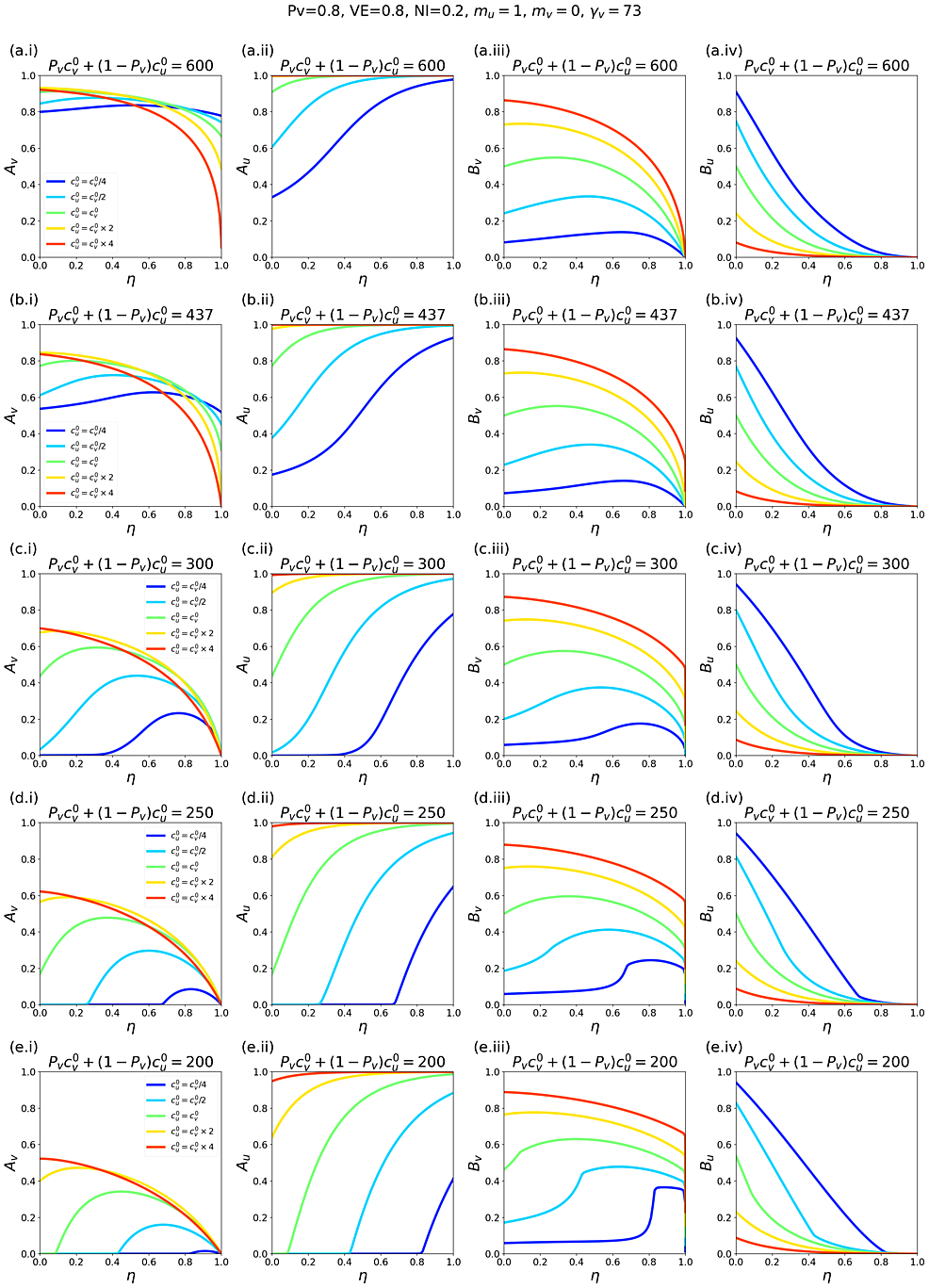
Appendix 2 contains supplementary figures with results for different parameter combinations, including P_v ≠ 0.8, m_v ≠ 0 and $c_{v}^{0} \neq c_{u}^{0}$ . In all results in this paper, simulations were initiated with a seed number of 100 infectious individuals distributed proportionately among the two sub-populations.

Results

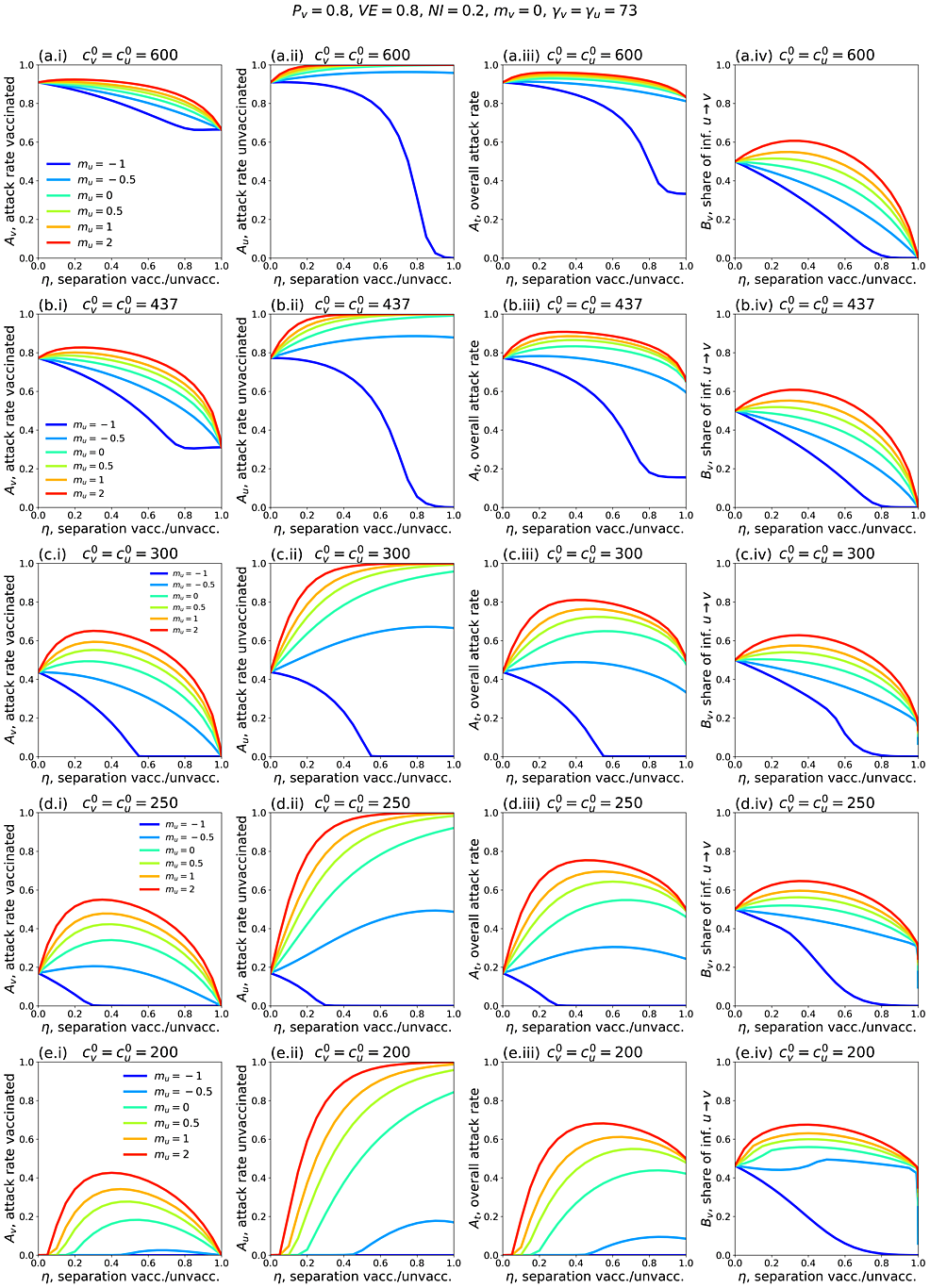
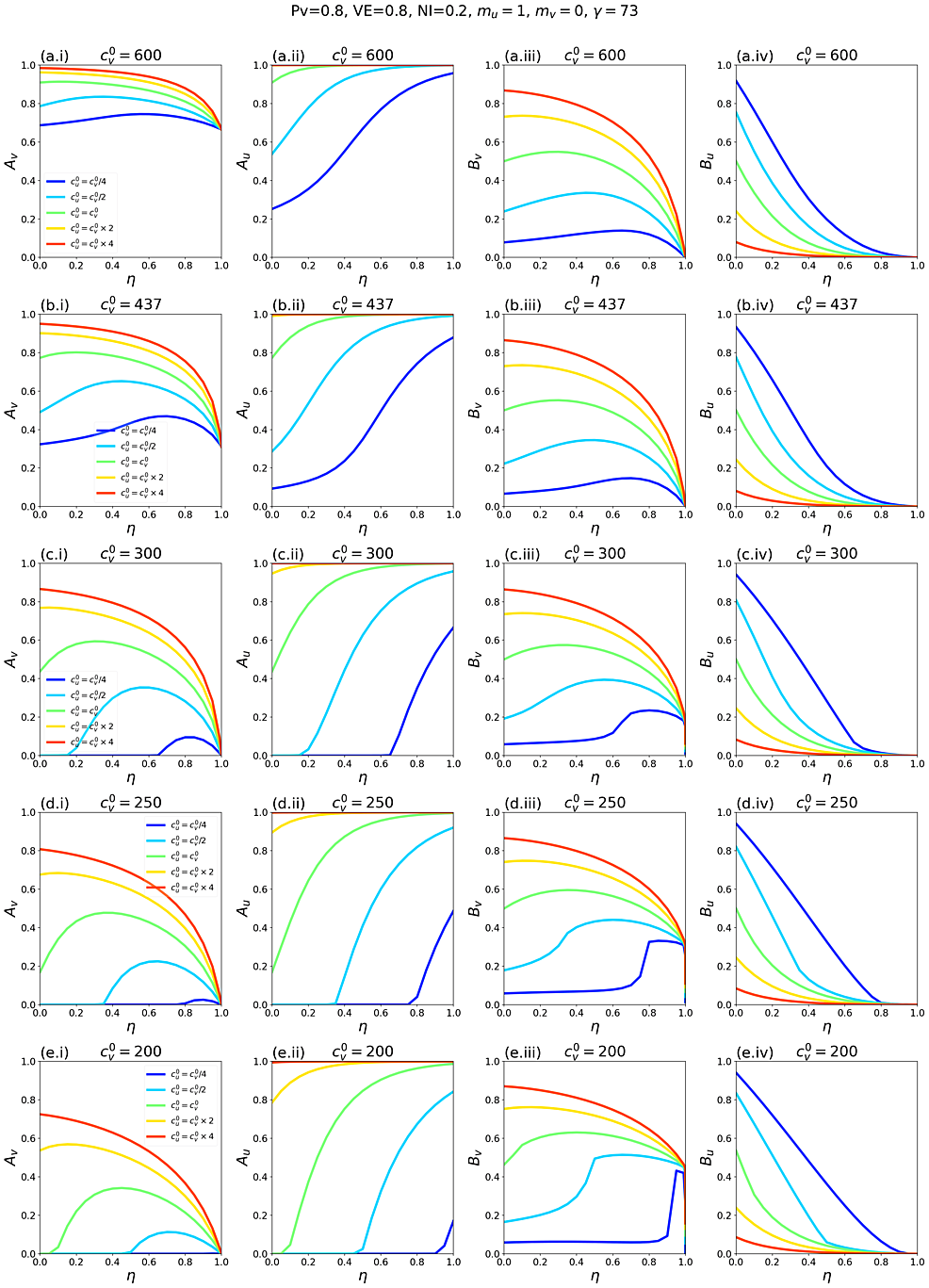
Figure 1 shows simulation results for a range of model parameters for different epidemiological conditions and degrees and types of societal segregation. Each row of panels is for a fixed value of $c_{v}^{0} = c_{u}^{0}$ , which decreases moving from the top row (Figures 1a.i-iv) to the bottom (Figures 1e.i-iv). The left column of panels shows how the attack rate among the vaccinated population, A_v, changes with the degree of segregation, η. The second and third columns show A_u and A_t as functions of η, respectively, and the right column shows how B_v, the share of vaccinated infections that were due to contacts with unvaccinated people, varies with η.

Figure 1: Attack rates as functions of the degree of segregation of vaccinated and unvaccinated populations

Attack rates A_v (vaccinated population), A_u (unvaccinated population), A_t(overall population) and share of vaccinated infections that were due to contacts with unvaccinated people, B_v, as functions of the degree of segregation, η, between the vaccinated and unvaccinated. Each row of panels shows A_v, A_u, A_t and B_v for a particular choice of $c_{v}^{0} = c_{u}^{0}$ . Values of fixed model parameters are indicated at the top of the figure. For reference, in a single-population (no vaccination) model, the corresponding R₀ values for rows a-e of the figure are 8.2, 6.0, 4.1, 3.4 and 2.7, respectively.

Figures 1c.i-iv show results for a moderate value of contacts per year. For reference, in a single-population (no vaccination) model, $c_{v}^{0} = c_{u}^{0}$ = 300 contacts/year and γ_v = γ_u = 73 years^-1 corresponds to a basic reproduction number R₀ = c/γ = 4.1.

In Figure 1c.i, when m_u =-1 and m_u = -0.5 (reflecting large and moderate degrees of exclusion and isolation of unvaccinated people), the vaccinated attack rate, A_vdecreases with increasing segregation. However, when m_u > 0 (compounding of unvaccinated people) or m_u = 0 (segregation has no influence on contact frequency of unvaccinated people), there is a maximum in A_v for moderate values of η. Therefore, with compounding segregation, large values of η are required for A_v to be lower than its value for no segregation (η = 0). Figure 1c.ii shows that the unvaccinated attack rate, A_u, increases with segregation for anything other than strong isolating segregation (m_u approaching -1). This produces a maximum in the overall attack rate, A_t, at moderate degrees of segregation, even for values of m_u for which A_v decreases monotonically (m_u = -0.5). Figure 1c.iv shows that B_v, the share of vaccinated infections that are due to unvaccinated people, has a shape similar to A_v(η, m_u). In all panels, 20% of the total population is unvaccinated (P_v = 0.8; Table 1).

Figures 1c.i-iv, therefore, demonstrate that whether applying segregation increases or decreases the vaccinated population attack rate depends on both the degree of segregation and how segregation affects contact frequency.

Figures 1a.i-iv and Figures 1b.i-iv show results for larger $c_{v}^{0} = c_{u}^{0}$ . Compared to Figure 1c.i, in Figure 1a.i and Figure 1b.i, A_v does not increase much with η when m_u > 0, and A_v no longer has a maximum when m_u = 0. It can also be seen that A_v increases with increasing $c_{v}^{0} = c_{u}^{0}$ when there is no segregation (η = 0).

Reducing $c_{v}^{0} = c_{u}^{0}$ (Figures 1d.i-iv and Figures 1e.i-iv) decreases A_v(η = 0), and larger η can dramatically increase A_v. Even with an isolating segregation policy (m_u = −0.5 in Figure 1d.i), A_v is increased for moderate values of η.

When $c_{v}^{0} = c_{u}^{0}$ are small enough, ( $c_{v}^{0} = c_{u}^{0}$ = 200 contacts/year in Figure 1e.i, corresponding to R₀ = 2.7 in a single population (no vaccination) model), there is no epidemic among the vaccinated in the absence of segregation (A_v(η = 0) = 0). However, a non-zero vaccinated-population attack rate (A_v > 0) occurs if η is sufficiently large, and emerges regardless of whether one isolates or compounds the unvaccinated. Therefore, for small enough values of
$c_{v}^{0} = c_{u}^{0}$ , any segregation could increase infections among the vaccinated.

The main qualitative features of the above results for P_v = 0.8 hold for other values of P_v. Appendix 2 provides a detailed exploration of results for P_v = 0.1 through 0.99; and for two values of VE (0.4 and 0.8). When VE is decreased, A_v is not strongly influenced by η, regardless of m_u; therefore, any beneficial effect of segregation on A_v is reduced as VE decreases.

Appendix 2 also explores $c_{v}^{0} \neq c_{u}^{0}$ . For example, when $c_{v}^{0} > c_{u}^{0}$ , the unvaccinated contact frequency is reduced even when there is no segregation; increasing η can then increase A_v substantially compared to the case of $c_{v}^{0} = c_{u}^{0}$ , holding all other parameter values constant (see panels a.i and b.i in figures A2.28 and A2.31 in Appendix 2).

Discussion

Segregation can have substantially different and negative impacts on the outcome of an epidemic, depending on the type and degree of segregation, and depending on cultural and population-density factors, for example, that co-determine $c_{v}^{0}$ and $c_{u}^{0}$ .

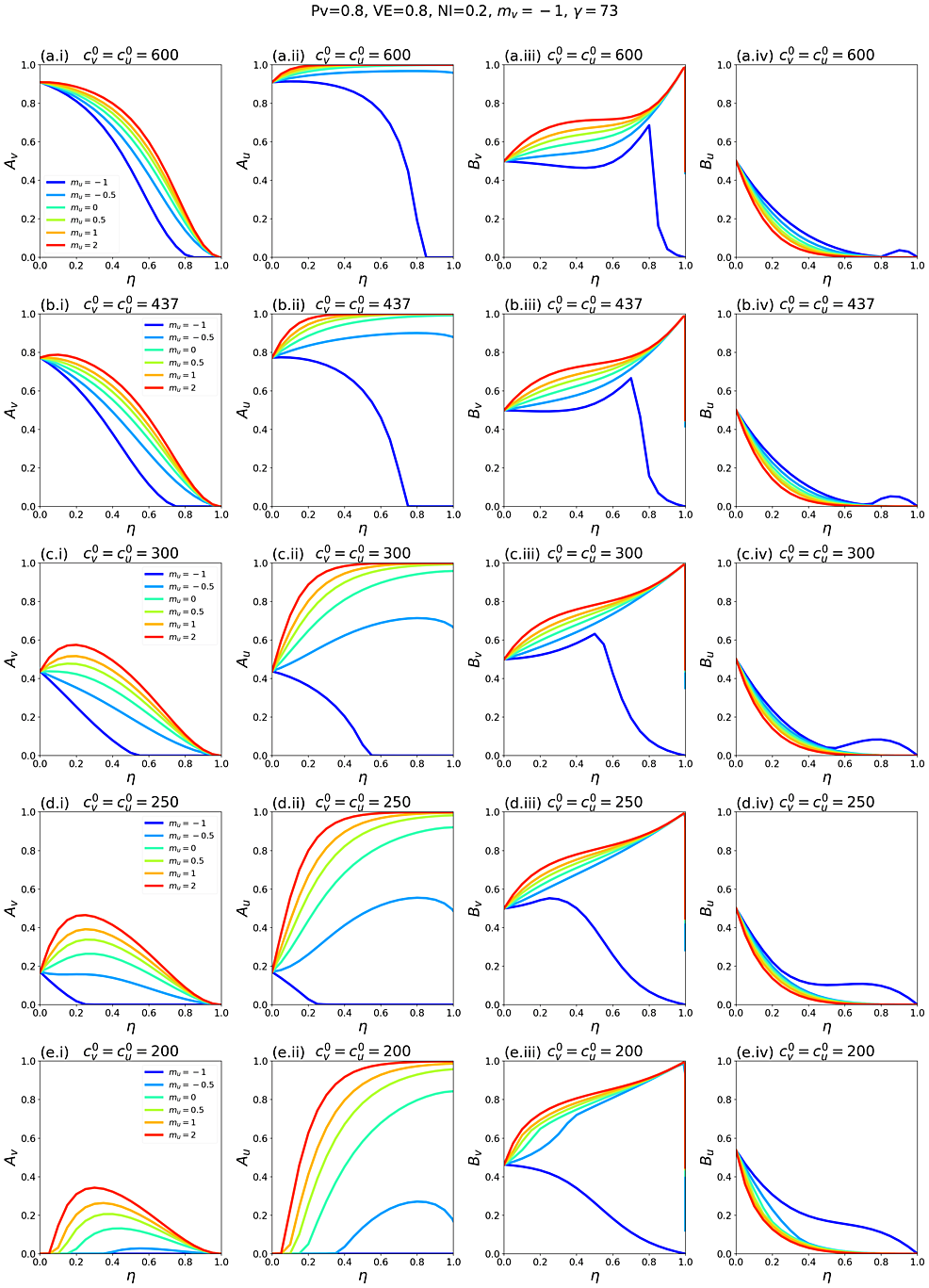
Segregation that compounds the unvaccinated (m_u > 0 and m_v = 0) generally causes an increase in the vaccinated-population attack rate, A_v, for small and intermediate degrees of segregation, η, while for large η, A_v decreases below its value in an unsegregated society. Segregation that isolates and excludes the unvaccinated (m_u < 0 and m_v = 0) decreases A_v for “more contagious viruses” (i.e. large $c_{v}^{0} = c_{u}^{0}$ , large R₀); however, for “less contagious viruses” (smaller $c_{v}^{0} = c_{u}^{0}$ , smaller R₀), both isolating and compounding types of segregation can increase A_v beyond its value in an unsegregated society. For “viruses that are not very contagious” (small $c_{v}^{0} = c_{u}^{0}$ , small R₀), applying segregation can cause a sizeable epidemic among the vaccinated even though virtually no vaccinated people would be infected in an unsegregated society. Segregation increases the unvaccinated attack rate, A_u, for compounding and moderately isolating types of segregation, and A_u is only decreased for strongly isolating segregation (m_uapproaching -1).

Except for large negative values of m_u, and small unvaccinated population fractions, applying segregation has the effect of increasing the frequency of unvaccinated-to-unvaccinated contacts (see figure A1.2 in Appendix 1). This increases the overall probability of a susceptible-infectious interaction, since the unvaccinated population has a higher fraction of susceptibles, and creates a form of core group dynamics [24-26]. At the same time, increasing segregation shields the vaccinated population from the increased prevalence of infection in the unvaccinated population. This trade-off causes the non-monotonic relationship between A_v and η. The same dynamic causes the emergence of an epidemic for large η when $c_{v}^{0} = c_{u}^{0}$ (and thus R₀) is small.

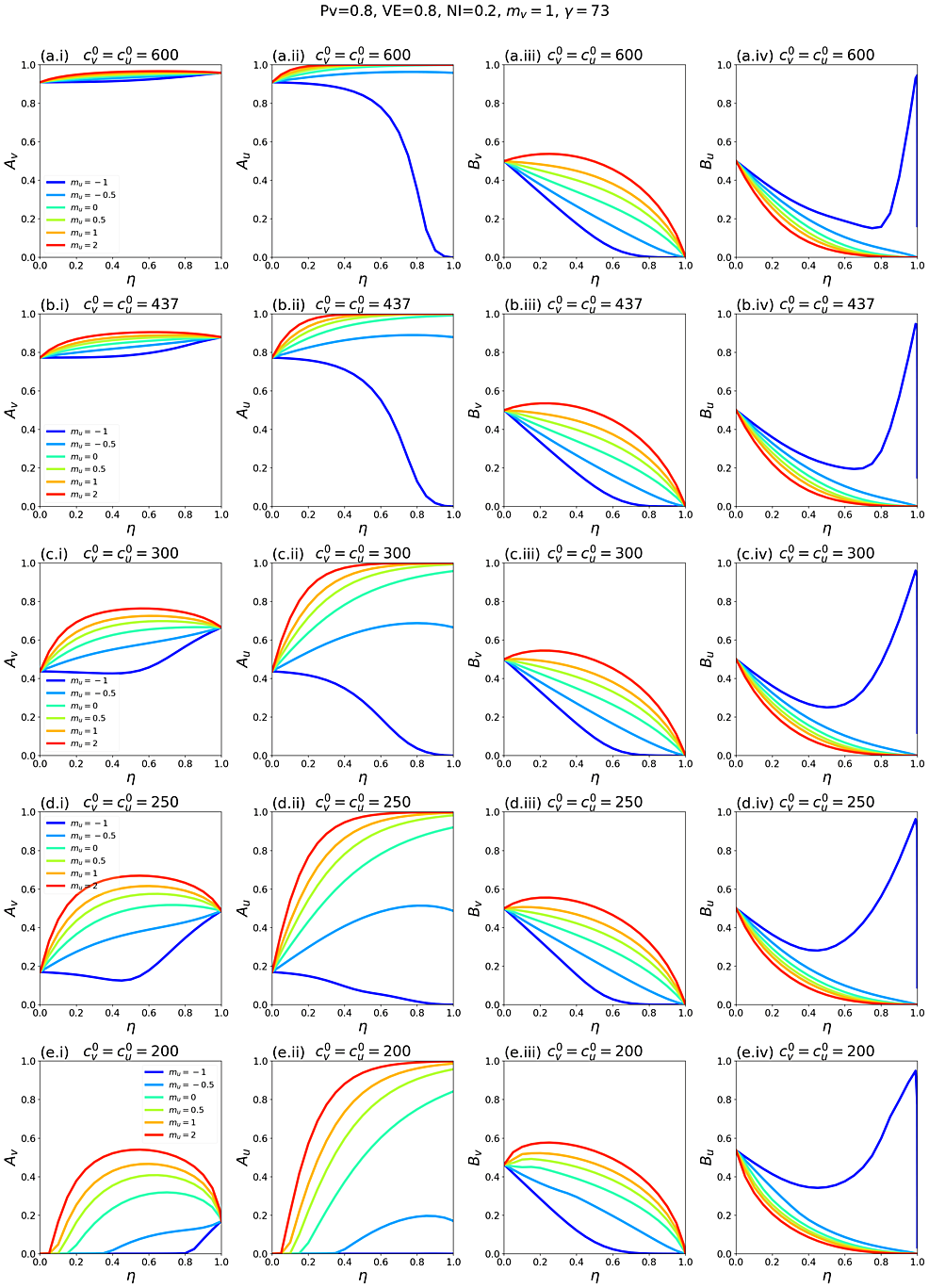
We find that B_v, the share of vaccinated infections that are due to contact with unvaccinated people, follows a similar trend to A_v as a function of the degree of segregation, when segregation has no impact on the vaccinated contact frequency (m_v = 0). For this type of segregation, A_v and B_v either increase or decrease simultaneously with increasing η, depending on the value of m_u, and B_v is minimized for complete segregation. When m_v = 0, there is no type or degree of segregation that reduces the vaccinated attack rate while simultaneously increasing the risk to vaccinated people from unvaccinated people (Figure 1). Therefore, there are no circumstances in which the unvaccinated cause a disproportionate risk to the vaccinated, contrary to conclusions in Fisman et al. [9].

In contrast, when m_v ≠ 0, such that segregation affects the contact frequencies of vaccinated people, increasing segregation can cause A_v to increase while B_vdecreases and vice-versa (see figures A2.25 and A2.26 in Appendix 2).

The impact of vaccination-status-based societal segregation on contact frequencies has not previously been considered to our knowledge, even in network-based models in which unvaccinated people cluster together in “cliques” or households [27-29].

Limitations

Our model assumes only two risk populations (vaccinated and unvaccinated), considers only the attack rates on epidemic completion (A_v, A_u, and A_t), and takes the degree of segregation η to be time-independent, without variation due to public holidays and such. It does not consider other outcomes such as death or hospitalization, and does not include different age groups with different characteristics such as contact frequencies or recovery times. Our model assumes an all-or-nothing VE, without waning immunity or influence on infectiousness; and no possibility of reinfection. We do not consider the impact of segregation policies on vaccination rates. SIR models and their variations are based on the paradigm of transmission due to pairwise contact between a recently infected and a susceptible individual. However, this paradigm is unable to account for important features of viral respiratory disease incidence; in particular, its rapid emergence and disappearance occurring at essentially the same time at widely dispersed locations [30]. Air-borne transmission via suspended aerosol particles is not directly compatible with pairwise transmission, since it occurs in built environments where many people may transit or be present [31]. A related and unavoidable limitation is the lack of reliable empirical evaluations of needed infectious contact frequencies, which is important because our calculated outcomes are sensitive to the chosen contact frequency values. Lastly, we do not consider the deleterious health impacts of the segregation policies themselves, which can be significant [32-38].

Conclusions

In the two-population mixing-model framework, vaccination-status-based societal segregation can lead to substantially different and counter-intuitive epidemic outcomes depending on the type and degree of segregation, and depending on complex cultural and physical factors that co‑determine infectious contact frequencies (i.e., the products βc). Negative epidemiological consequences can occur for either segregated group, irrespective of the deleterious health impacts of the policies themselves.

Given the lack of reliable empirical evaluations of needed infectious contact frequency values, the demonstrated outcome sensitivities to the infectious contact frequencies, and the intrinsic limitations of SIR models in this application, we cannot recommend that SIR modelling be used to motivate or justify segregation policies regarding viral respiratory diseases, in the present state of knowledge.

References

Garnett GP, Anderson RM: Sexually transmitted diseases and sexual behavior: insights from mathematical models. J Infect Dis. 1996, 174:S150-61. 10.1093/infdis/174.supplement_2.s150
Siegenfeld AF, Taleb NN, Bar-Yam Y: Opinion: what models can and cannot tell us about COVID-19. Proc Natl Acad Sci U S A. 2020, 117:16092-5. 10.1073/pnas.2011542117
Hethcote HW: The mathematics of infectious diseases. SIAM Rev Soc Ind Appl Math. 2000, 42:599-653. 10.1137/S0036144500371907
Keeling MJ, Rohani P: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, Princeton; 2008.
Martcheva M: An Introduction to Mathematical Epidemiology. Springer, New York; 2015.
Garnett GP, Anderson RM: Balancing sexual partnerships in an age and activity stratified model of HIV transmission in heterosexual populations. IMA J Math Appl Med Biol. 1994, 11:161-92. 10.1093/imammb/11.3.161
Nold A: Heterogeneity in disease-transmission modeling. Math Biosci. 1980, 52:227-40. 10.1016/0025-5564(80)90069-3
Hickey J, Rancourt DG: Predictions from standard epidemiological models of consequences of segregating and isolating vulnerable people into care facilities. PLoS One. 2023, 18:e0293556. 10.1371/journal.pone.0293556
Fisman DN, Amoako A, Tuite AR: Impact of population mixing between vaccinated and unvaccinated subpopulations on infectious disease dynamics: implications for SARS-CoV-2 transmission. CMAJ. 2022, 194:E573-80. 10.1503/cmaj.212105
Virk N: Epidemic Modeling of a Simple Respiratory Pathogen [Thesis]. University of British Columbia, Vancouver, BC; 2022. 10.14288/1.0417535
Kosinski RJ: The failures of an ideal COVID-19 vaccine: a simulation study [PREPRINT]. medRxiv. 2021, 10.1101/2021.11.22.21266669
Fisman DN, Amoako A, Simmons A, et al.: Impact of immune evasion, waning and boosting on dynamics of population mixing between a vaccinated majority and unvaccinated minority [PREPRINT]. medRxiv. 2023, 10.1101/2023.02.03.23285437
Morris M: A log-linear modeling framework for selective mixing. Math Biosci. 1991, 107:349-77. 10.1016/0025-5564(91)90014-A
Chuan Voo T, Savulescu J, Schaefer O, Ho Zhi Ling A, Tam CC: COVID-19 differentiated measures for unvaccinated individuals: the need for clear goals and strong justifications. Vaccine. 2022, 40:5333-7. 10.1016/j.vaccine.2022.06.051
Ward JK, Gauna F, Gagneux-Brunon A, et al.: The French health pass holds lessons for mandatory COVID-19 vaccination. Nat Med. 2022, 28:232-5. 10.1038/s41591-021-01661-7
Wang B, Ping Y: A comparative analysis of COVID-19 vaccination certificates in 12 countries/regions around the world: rationalising health policies for international travel and domestic social activities during the pandemic. Health Policy. 2022, 126:755-62. 10.1016/j.healthpol.2022.05.016
Bardosh K, de Figueiredo A, Gur-Arie R, et al.: The unintended consequences of COVID-19 vaccine policy: why mandates, passports and restrictions may cause more harm than good. BMJ Glob Health. 2022, 7:10.1136/bmjgh-2022-008684
COVID-19 Designated Quarantine Facilities: Staying at the facility. (2023). Accessed: October 25, 2023: https://travel.gc.ca/travel-covid/travel-restrictions/isolation/designated-quarantine-facilities#archived.
Travelling to or within Canada? The Rules Have Changed. Here’s What You Need to Know. (2021). Accessed: October 25, 2023: https://www.cbc.ca/news/business/travel-rules-canada-government-1.6105707.
Queensland’s Wellcamp COVID Quarantine Facility to Take First Arrivals This Weekend. (2022). Accessed: October 25, 2023: https://www.abc.net.au/news/2022-02-04/covid-queensland-wellcamp-quarantine-facility-first-guests/100804636.
Looi MK: Vaccine passports around the world. BMJ. 2021, 374:n2142. 10.1136/bmj.n2142
Wölfel R, Corman VM, Guggemos W, et al.: Virological assessment of hospitalized patients with COVID-2019. Nature. 2020, 581:465-9. 10.1038/s41586-020-2196-x
Isolation and Precautions for People with COVID-19. (2023). Accessed: October 25, 2023: https://www.cdc.gov/coronavirus/2019-ncov/your-health/isolation.html.
Hadeler KP, Castillo-Chavez C: A core group model for disease transmission. Math Biosci. 1995, 128:41-55. 10.1016/0025-5564(94)00066-9
Boily MC, Lowndes C, Alary M: The impact of HIV epidemic phases on the effectiveness of core group interventions: insights from mathematical models. Sex Transm Infect. 2002, 78 Suppl 1:i78-90. 10.1136/sti.78.suppl_1.i78
Brauer F, Castillo-Chavez C, Feng Z: Models with heterogeneous mixing (chapter 5). Mathematical Models in Epidemiology. Springer, New York; 2019. 179-225.
Salathé M, Bonhoeffer S: The effect of opinion clustering on disease outbreaks. J R Soc Interface. 2008, 5:1505-8. 10.1098/rsif.2008.0271
De-Leon H, Aran D: Over- and under-estimation of vaccine effectiveness [PREPRINT]. medRxiv. 2023, 10.1101/2022.01.24.22269737
Achitouv I: Propagation of epidemics in a polarized society: impact of clustering among unvaccinated individuals [PREPRINT]. arXiv. 2022, 10.48550/arXiv.2206.00357
Hope-Simpson RE: The Transmission of Epidemic Influenza. Springer, New York; 1992. 10.1007/978-1-4899-2385-1
Bulfone TC, Malekinejad M, Rutherford GW, Razani N: Outdoor transmission of SARS-CoV-2 and other respiratory viruses: a systematic review. J Infect Dis. 2021, 223:550-61. 10.1093/infdis/jiaa742
Cohen S: Social relationships and health. Am Psychol. 2004, 59:676-84. 10.1037/0003-066X.59.8.676
Cohen S, Tyrrell DA, Smith AP: Psychological stress and susceptibility to the common cold. N Engl J Med. 1991, 325:606-12. 10.1056/NEJM199108293250903
Cohen S, Doyle WJ, Skoner DP: Social ties and susceptibility to the common cold. JAMA. 1997, 277:1940-4. 10.1001/jama.1997.03540480040036
Holt-Lunstad J, Smith TB, Layton JB: Social relationships and mortality risk: a meta-analytic review. PLoS Med. 2010, 7:e1000316. 10.1371/journal.pmed.1000316
Holt-Lunstad J, Smith TB, Baker M, Harris T, Stephenson D: Loneliness and social isolation as risk factors for mortality: a meta-analytic review. Perspect Psychol Sci. 2015, 10:227-37. 10.1177/1745691614568352
Valtorta NK, Kanaan M, Gilbody S, Ronzi S, Hanratty B: Loneliness and social isolation as risk factors for coronary heart disease and stroke: systematic review and meta-analysis of longitudinal observational studies. Heart. 2016, 102:1009-16. 10.1136/heartjnl-2015-308790
Elovainio M, Hakulinen C, Pulkki-Råback L, et al.: Contribution of risk factors to excess mortality in isolated and lonely individuals: an analysis of data from the UK Biobank cohort study. Lancet Public Health. 2017, 2:e260-6. 10.1016/S2468-2667(17)30075-0

Appendices

Appendix 1

https://figshare.com/articles/preprint/Appendix_1_of_the_pre-print_Compartmental_mixing_models_for_vaccination-status-based_societal_separation_regarding_viral_respiratory_diseases_by_J_Hickey_D_G_Rancourt_posted_to_medRxiv_on_2023-07-19_Version_4_https_www_medrxiv_org_content_1/24431836

Figure 2: Figure A1.2 from Appendix 1

Normalized population-specific contact frequencies c_u and c_v, intra-population contact frequencies c_uu and c_vv, and inter-population contact frequencies c_uv and c_vu, as functions of η, for the six values of m_u explored in the main text (each row of panels corresponds to a different value of m_u), for m_v = 0, and for P_v = 0.2 (left column of panels), P_v = 0.5 (middle column) and P_v = 0.8 (right column).

Appendix 2

https://figshare.com/articles/preprint/Appendix_2_of_the_pre-print_Compartmental_mixing_models_for_vaccination-status-based_societal_separation_regarding_viral_respiratory_diseases_by_J_Hickey_D_G_Rancourt_posted_to_medRxiv_on_2023-07-19_Version_4_https_www_medrxiv_org_content_1/24431848

Figure 3: Figure A2.25 from Appendix 2

A_v, A_u, B_v, and B_u and functions of η. Each row of panels corresponds to a single choice of $c_{v}^{0} = c_{u}^{0}$ , and each coloured line to a choice of m_u as indicated in the legends. Parameter values P_v=0.8, VE=0.8, NI=0.2, m_v=0, m_u = 1, γ_v = γ_u = 73. This figure is the same as Fig. 1 in the main text, except that m_v = 1.

Figure 4: Figure A2.26 from Appendix 2

Same as Fig. A2.25 from Appendix 2, except that m_v = -1.

Figure 5: Figure A2.28 from Appendix 2

$c_{v}^{0} \neq c_{u}^{0}$ , m_v = 0, m_u = 1, γ_v = γ_u = 73, VE = 0.8, NI = 0.2, various choices of $c_{v}^{0} / c_{u}^{0}$ (see legend within left-column panels), showing A_v, A_u, B_v, and B_u as functions of η. $c_{v}^{0}$ is fixed for each row in the figure and decreases moving down the rows.

Figure 6: Figure A2.31 from Appendix 2

$c_{v}^{0} \neq c_{u}^{0}$ , m_v = 0, m_u = 1, γ_v = γ_u = 73, VE = 0.8, NI = 0.2, various choices of $c_{v}^{0} / c_{u}^{0}$ (see legend within left-column panels), showing A_v, A_u, B_v, and B_u as functions of $η$ . The weighted sum $P_{v} c_{v}^{0} + (1 - P_{v}) c_{u}^{0}$ is fixed for each row and decreases moving down the rows.

Better in their words…